The ball flight is a physical phenomenon witnessed by golfers endless of times. It is however very seldom related to in context of the aerodynamics and forces involved in describing the ball flight. This article aims to give a solid foundation to the physical background of the ball flight, so that every golfer can relate changes in the ball flight to the physics causing it.
The supporting physics for the analysis can be found in the appendix.
Analysing flights in the wind
To predict ball flights under the influence of wind, we can apply the wind profile from the appendix and add the wind speed to the ball speed to get a ball relative air speed. This relative value is the speed of the air passing over the ball and is the speed that give rise to the drag and lift force. Following is an analysis for how a PGA average 7-iron is affected by the 10 mph wind profile seen in Figure 8 in the appendix. From there we, then compare how a knocked-down shot would perform under the same conditions and apply our knowledge about drag and lift forces along with wind profiles to explain what it is considered as an efficient flight for windy conditions.
The updated trackman averages give launch conditions, 123 mph ball speed, 7124 RPM and launch angle of 16.1° (Trackman, 2024). From the ball flight model used in tGAT the base-line 7-iron give the flights in Figure 1 with the specific flight data found in table 1.
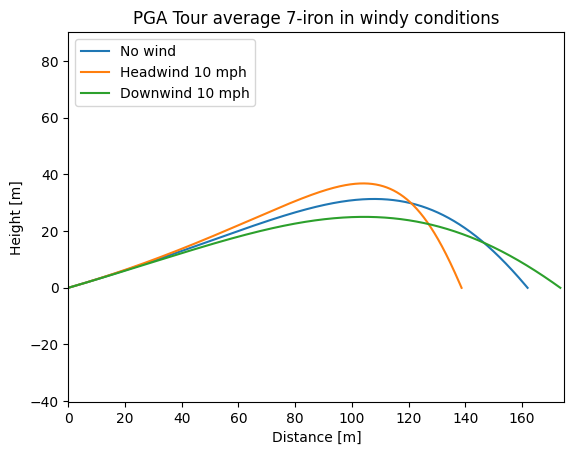
| Headwind | No wind | Downwind | |
| Carry | 139 m | 162 m | 174 m |
| Height | 37 m | 32 m | 25 m |
| Descent | 67 ° | 50 ° | 36 ° |
What can be noted by looking at the numbers is that the carry is reduced by 23 m when the wind is into but only increased by 12 m when its downwind. This effect that headwind hurt more on distance then downwind help is often spoken about in golf. If we instead look at the peak heights we see that the downwind actually pushes the ball down more than the headwind lifts it up. This means that the downwind 7-iron get a descent angle of only 36 ° which is a problem if the greens are firm. Conversely, for the headwind the descent angle is a lot higher than necessary.
Considering the noticeable differences in the three flights, its apparent that any uncertainty in wind direction or strength will cause problems with proximity with approach shots. One alternative to the stock 7-iron in windy conditions is the knocked-down shot. Its primary purpose is in the headwind case so the following shot is designed to go a similar length into the wind as the stock 7-iron. This is so that we can do a relevant comparison. The launch conditions chosen to recreate a carry around 139 m in 10 mph headwind is a launch of 12 °, spin of 5000 RPM and a ball speed of 116 mph. Figure 2 show the three new flights and table 2 show the new flight data.
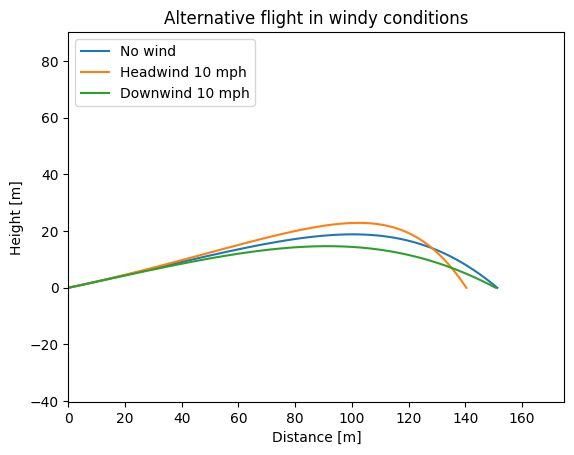
| Headwind | No wind | Downwind | |
| Carry | 140 m | 151 m | 151 m |
| Height | 23 m | 19 m | 15 m |
| Descent | 56 ° | 40 ° | 28 ° |
At first glance we can see that the carry for the three cases are all within 11 m of each other compared to the range of 35 m seen for the stock 7-iron. Furthermore, we can see that the peak heights and descent angles have all decreased. As a mean of reducing the proximity to the hole, we can deduce that this flight would still end up close if we had an unreliable gusty wind or trees nearby that cast doubt to the actual strength and direction of the wind. Our limitations are however dependent upon the descent angle which limits when the shot can be used.
Why this flight is more efficient in the wind comes down to a hand full of effects. Firstly, the wind profile indicate that a potential error in our estimate of the wind strength or direction is magnified if we hit it higher as the strength of the wind increases with height. So, by hitting it lower there is less wind which can have an affect. One efficient way to reduce the height is to reduce the spin rate. This have a two fold effect: reduced CL, which means reduced lift force that pushes the ball up, but also reduced CD, as CD decrease if the spin is reduced. This reduce in CD is what makes the ball fly “through” the wind better. The next way to reduce the height is to simply decrease the launch angle. An added bonus to this is that the ball has a higher speed through the apex which means that it spend less time around the apex where the transition of airflow increase CD. That is, less time at the part of the flight where it is the most subjected to the wind but at the same time the ball has a slightly higher speed at that location which reduces the CD and give it more of a “fly through the wind effect”. Lastly, by reducing the ball speed we have the added benefits of reducing the lift force through the first half of the flight and keeping the ball lower as an effect. It also keeps the ball lower as its initial vertical speed is less and thus less force over time is required to get it flying downwards by Newton’s second law of motion (ΣF = ma).
As mentioned before, the use of this shot comes down to when the descent angle allows for it. For softer greens which are deeper front-to-back and preferably also with slope towards the line of play, a shallower descent angle still works. If the situation of the green is the reverse, arguments dictate that the launch, spin, and ball speed should, if necessary, instead work in the opposite direction from the knocked-down shot to give a descent angle with the possibility of stopping the ball.
Ball flight in tGAT
In tGAT the ball flight model also include components that makes it possible to analyse effects in 3D. The wind direction can be turned a full 360 ° around, ground-level can be altered to simulate uphill or downhill approaches and start direction and spin axis makes it possible to create draws and fades. One thing to note about the spin axis is that all it does is to turn the direction that the lift force, FL acts in.
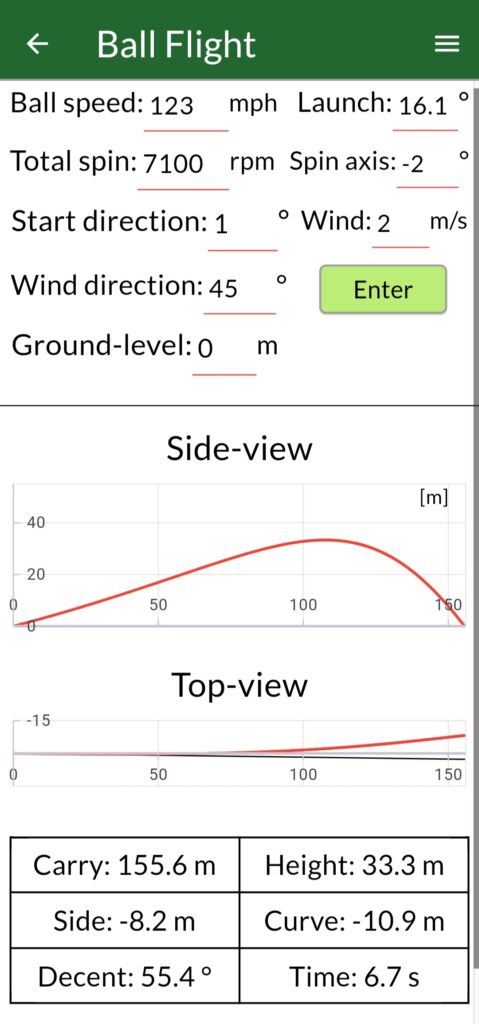
Appendix
The supporting physics recommended to fully grasp the ideas and concepts presented in the analysis.
Equations
The main equations that will be used to describe the flight of the ball will be introduced in this section and then referenced to when discussing flight characteristics later on.
Firstly, we have Newton’s second law of motion which states that the sum of the forces acting on an object is equal to it’s mass multiplied by it’s acceleration. ΣF = ma. From this equation we can get the acceleration of the golf ball which, taken over a time, will give both the ball’s velocity and position.
Secondly, we need expressions for the different forces acting on the golf ball to solve for the acceleration mentioned above. In this analysis we will stick to three forces. The drag force (air resistance), lift force (generated from spin and generally referred to as the Magnus effect ) and the force of gravity. The force from gravity, Fg, is simply Fg=mg, where g is the gravitational acceleration. The drag force, FD, can be expressed as FD=½CDρAV2 and acts in the opposite direction of the velocity. Where V is the speed of the ball relative the air, A is the cross-sectional area exposed to the wind face-on, ρ is the density of air, and CD is the drag coefficient. Similarly, the lift force, FL, can be expressed as FL=½CLρAV2 but it acts perpendicular to the velocity. CL is here the lift coefficient and A is instead the cross-sectional area viewed from the top (because of symmetry of a golf ball both areas are equal to the area of a circle A=r2π with radius, r). Figure 4 show the force diagram for the forces discussed above.
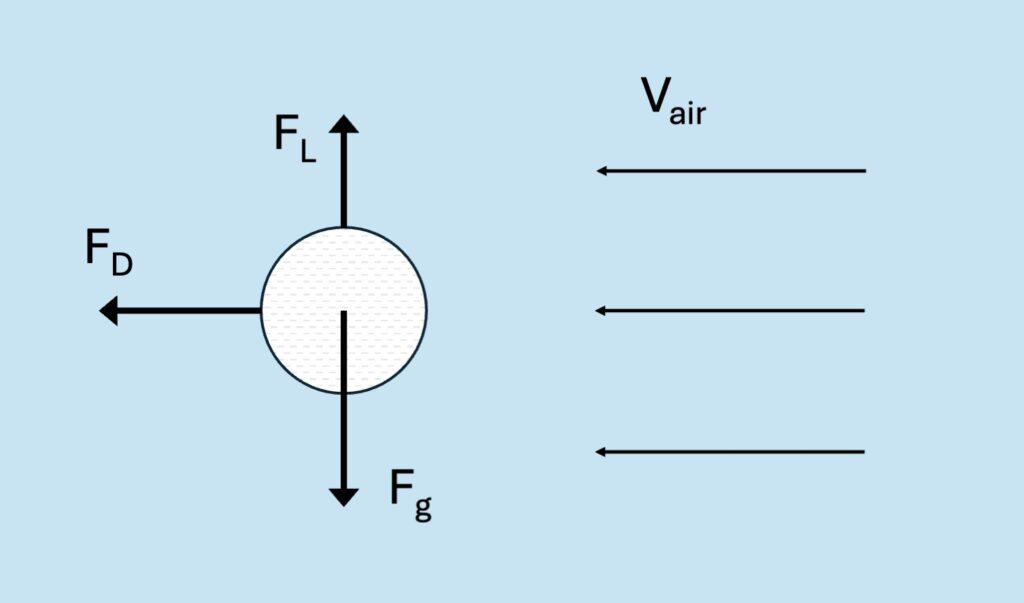
As both the drag and lift coefficients for different bodies are usually used in respect to the Reynolds number, Re, I’ll briefly mention it. Reynolds number is the quotient of dynamic forces and viscous forces, Re=ρLV/μ. Here L, is a characteristic length (for a sphere its the diameter), and μ is the dynamic viscosity of air. Since we are only discussing golf balls I’ll use standard air assumptions and discuss the lift and drag coefficients in respect to ball relative air speed in mph.
| r = 0.02135 m |
| m = 0.046 kg |
| g = 9.81 m/s2 |
| ρ = 1.2 kg/m3 |
| μ = 18.1×10-6 kg/ms |
Closer look at CD and CL
The force diagram in Figure 4 for a golf ball is actually the same force diagram that you would get for an airplane wing. But for the golf ball, the lift is generated though backspin whereas the wing generate it from its wing profile. This means that their flights would by all means not look the same and, hence, something must separate the golf ball from the wing. So, the two parameters that can vary between the two different cases, to give the unique flights, is the lift coefficient (CL) and drag coefficient (CD).
By looking at experimental data it is possible to get a good idea for how CD and CL will change depending on speed and spin rate. With these values, it is possible to create a model that predicts ball flight fairly accurately.
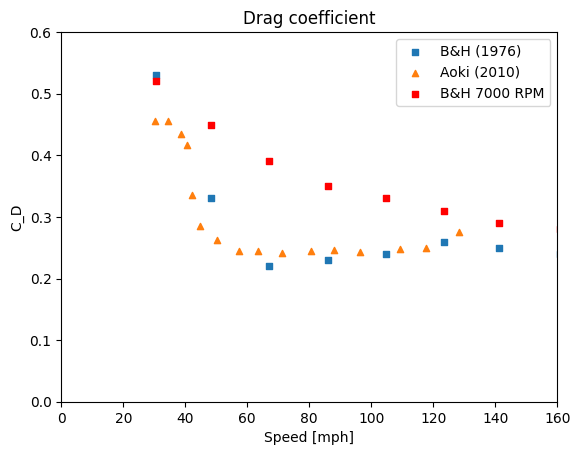
The drag coefficient is plotted against the ball speed in Figure 5 for experimental data gathered by Aoki et al. (2010) for zero spin and also Bearman and Harvey (1976) for zero spin and spin of 7000 RPM. What can be seen in Figure 5 is a noticeable decrease for CD at around 60 mph for zero spin. This has to do with the aerodynamics of the dimples that cause the airflow to transition from a laminar flow to a turbulent flow. For a blunt object such as a sphere, turbulent flow help reduce the size of the wake created behind the ball which is a considerable contributor to the drag force. In comparison, a smooth golf ball will instead transition to turbulent flow at around 230 mph, which is why they fly considerably shorter. What can also be seen in the experimental data is that the drag force increase with an increase in spin rate.
An effective method for displaying how CL change with speed and spin rate is to plot CL against the quotient for spin/speed [RPM/mph] as seen in Figure 6. What the data show is a close to linear relationship between the quotient and CL. This means that if the speed is held constant, an increase in spin rate linearly increase the lift coefficient. On the other hand, if spin is held constant an increase in speed would linearly reduce the lift coefficient.
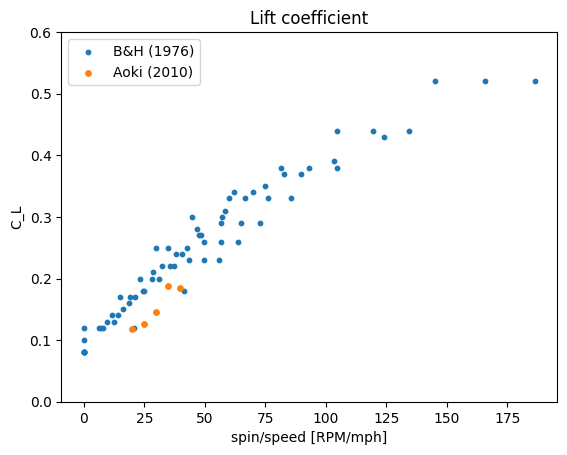
A few important take-aways from figures 5, 6 and the equations above. Firstly, as the spin rate usually decrease by less than 20 % for entire duration of the flight (Dewhurst, 2015) while the speed reduce substantially more the first half of the flight before the speed plateaus, the lift coefficient increase for the first half of the flight and then also plateaus. Secondly, the latter half of the flight is usually below 60 mph which means that the drag coefficient is a lot higher that half. This is what makes it possible to hit mid irons which fly far but still comes down soft with a steep descent angle. Lastly, even though both CD and CL have higher values for the second half of the flight, the size of FD and FL is less because of the lower speeds. An example, an average PGA Tour players 7-iron has a ball speed of 123 mph and spin of 7124 RPM at launch and at around the apex the speed has reduced to around 45 mph and the spin to around 6500 RPM. By looking at Figure 5 and using the data for 7000 RPM for CD we get our CD for launch to 0.3 and at around apex to 0.45. Figure 6 give CL for launch to 0.3 and to 0.45 at around apex. If we then convert our speeds to m/s and plug our numbers into our drag and lift force equation we get the following forces. FD at launch = 0.78N, FL at launch = 0.78N, FD at apex= 0.16N, FL at apex = 0.16N. The big difference in the size of the force comes from that the speed is squared in the equations and thus affect more. (That CD and CL had the same values at launch and around apex is more of a coincident than rule of thumb). For comparison of forces, the force from gravity Fg = 0.45N which means that the ball will climb in the beginning as FL at launch is greater than Fg.
Wind
As noted earlier, the speed of the ball has the greatest effect on the forces acting on the ball. So far we have only discussed the ball speed with no external wind effect but as golf is usually played subjected to the elements we need a way to incorporate it in our prediction.
Below 100 m the strength of the wind can be approximated by a logarithmic wind profile where the strength of the wind increases with height (The Swiss Wind Power Data Website, n.d.). Below is the equation used.
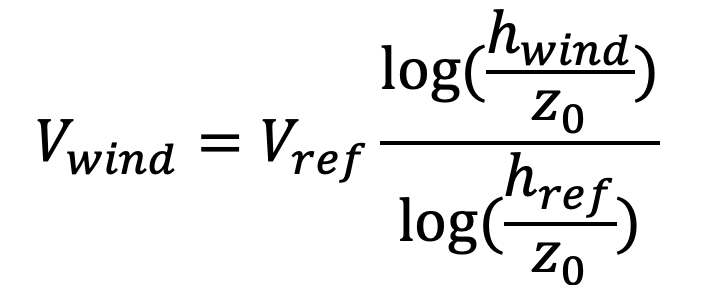
In the equation Vwind is the wind strength at a certain height, hwind. Vref is a known wind strength at a reference height, href, which is 2 m for our case. The last variable z0 is a roughness length which is an approximation of the terrain (z0 is set to 0.04 m which is an estimate for a fairly open golf course).
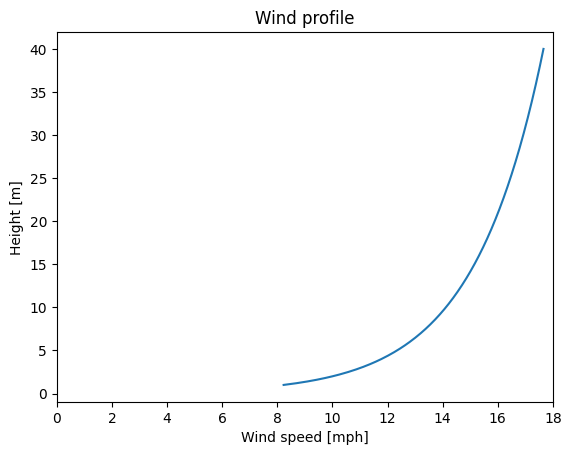
Figure 8 show what the wind profile look like for a 10 mph wind for the first 40 m above the ground.
References
Aoki, K., Muto, K., & Okanaga, H. (2010). Aerodynamic characteristics and flow pattern of a golf ball with rotation. Procedia Engineering, 2(2), 2431–2436. https://doi.org/10.1016/j.proeng.2010.04.011
Bearman, P. W., & Harvey, J. K. (1976). Golf ball aerodynamics. The Aeronautical Quarterly, 27(2), 112–122. https://doi.org/10.1017/S0001925900007617
Dewhurst, P. (2015). The science of the perfect swing. Oxford.
The Swiss Wind Power Data Website. (n.d.). Wind Profile Calculator. https://wind-data.ch/tools/profile.php
Trackman. (2024). Trackman tour averages. https://www.trackman.com/blog/golf/introducing-updated-tour-averages
Further reading
In the book The science of the perfect swing the author Peter Dewhurst looks further into how wind effect the ball flight. Covering the topics such as the effect on directional components from headwind, downwind and crosswinds but also a lot more golf related content.
