In this previous post I covered how it is possible to very accurately predict aim for putts on a 1-plane surface. That is, having a constant slope and elevation for the entire putt. In this post we will look into how it is possible to apply our green reading skills on a 1-plane surface to predict aim for 2-plane surfaces such as for example a double-breaker.
The definition used for a 2-plane surface in our context is as follows. The first ⅓ of the putt has a constant slope and elevation denoted slope1 and elevation1. Then a smooth linear transition appear for the next ⅓ of the putt to the new values for slope and elevation denoted slope2 and elevation2. For the last ⅓ of the putt and behind the hole, slope and elevation has the constant values of slope2 and elevation2.
Furthermore, we need to introduce the new concept of break-diagrams in order to better understand the underlying theory for 2-plane green reading. A break diagram show the break-rate on one axis which is defined as the speed that a tangent line to the path of the putt moves from the aim at the initial position to 0 cm when entering the hole [unit mm/dm]. On the other axis, the distance traveled towards the hole is shown.
Demonstrating by example, a traditional 1-plane surface putt with slope of 2%, elevation of 0%, distance of 3m and stimp 10 for a speed that takes it 40 cm past the hole and drop speed give the paths found in Figure 1 and break diagram found in Figure 2. The aim for 40 cm past is estimated to 27,6 cm and the aim for drop speed is estimated to 39,7 cm.
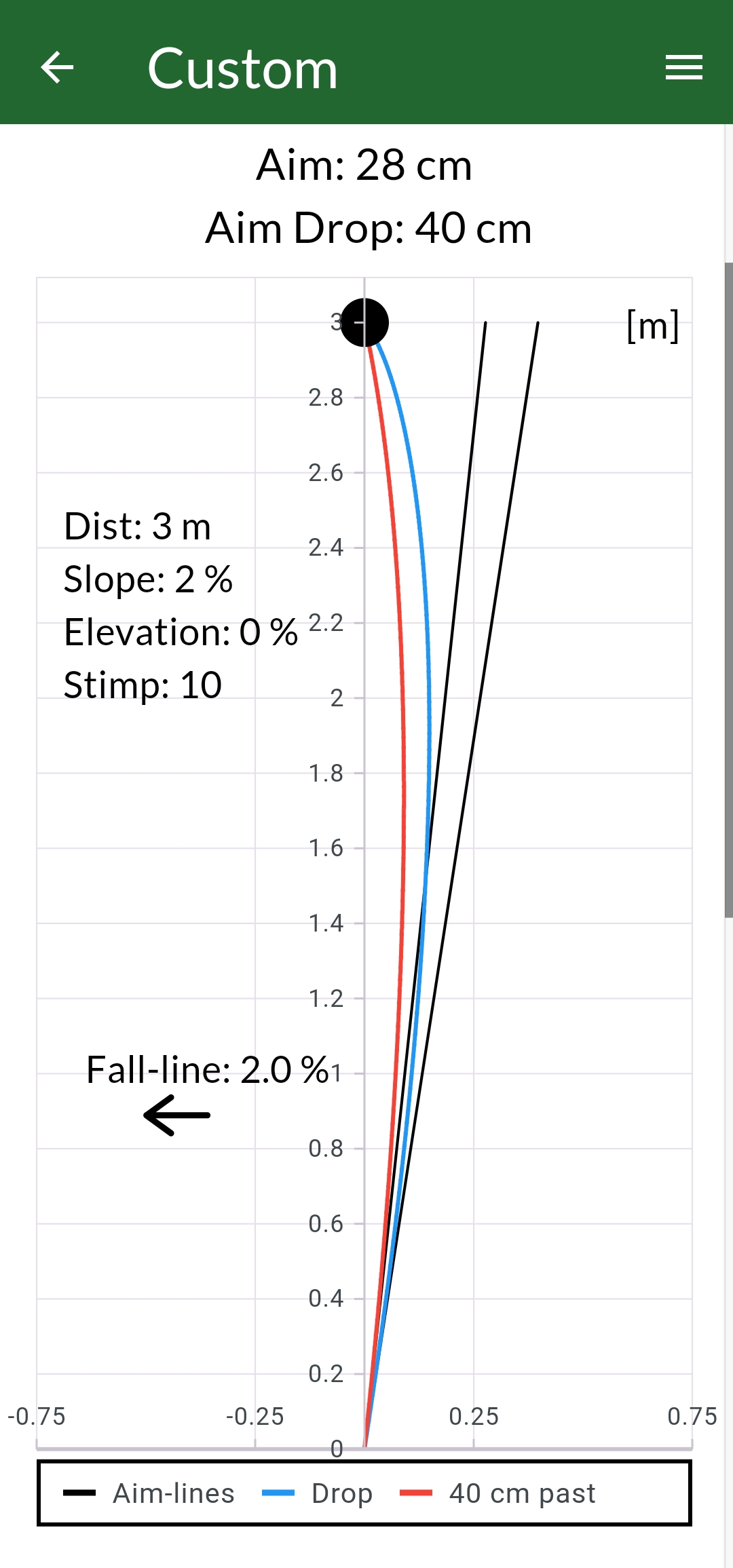
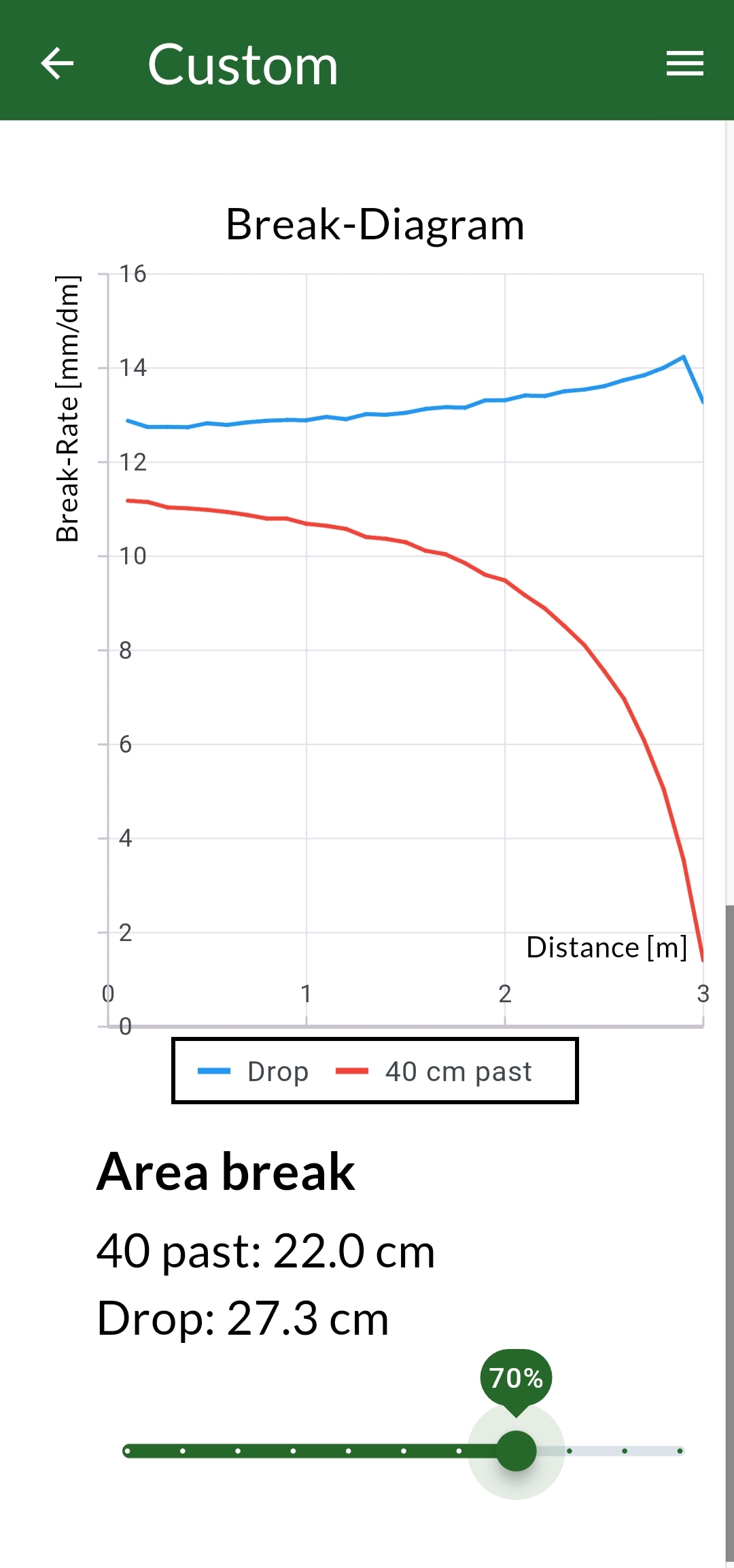
From the break diagram we get a few key insights. By looking at the areas underneath each graph we find that this correspond to the aim of the putt in cm. This makes it possible to compare areas to see “where break occurs”. For instance, by comparing the difference between the two paths we can make an estimate for where the extra break occurs. In this case we can predict that about 56% of the extra break by hitting the ball with drop speed occur in the last 0.9m of the putt.
If we do a similar analysis for a double-breaker with the characteristics and data seen in table 1, we get the following graphs.
| Slope1 | -2 % |
| Slope2 | 2 % |
| Elevation1 | 0 % |
| Elevation2 | 0 % |
| Distance | 3 m |
| Stimp | 10 |
| Aim 40 cm past | -4,7 cm |
| Aim drop speed | 0,6 cm |
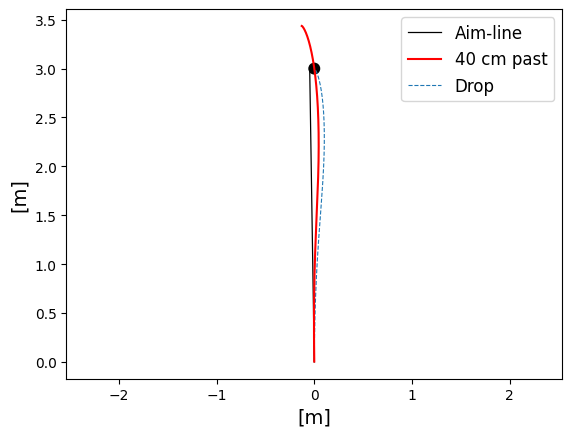
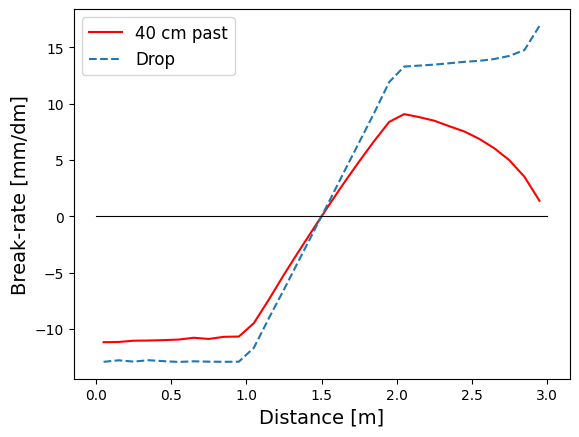
From the data in Table 1 we can see that the aim for 40 cm past the hole is negative (-4,7 cm) which would indicate that the slope for the first half of the putt has a greater affect on the total break. One intuitive explanation to why this occur, is that the distance to the hole plays a role in how much the seen curvature actually cause break. For example, by looking at the curvature for the 40 cm past the hole speed in Figure 1, it can be seen that it increases through the entire putt, but as the ball get closer to the hole its curvature has less space to move the ball away from the hole. In contrast, for the drop speed the curvature increases more dramatically when the speed gets close to zero which means that the distance to the hole effect is counteracted.
Also, by looking at the break diagram in Figure 4 it is possible to see that the negative area is larger for 40 cm past the hole speed whereas the opposite is true for drop speed.
By doing these types of analysis on many different 2-plane reads it is possible to create a general guideline for how to convert an arbitrary 2-plane read into a 1-plane surface which can be calculated using the tGAT green reading system. What you should do is to weigh in the importance for the different slopes and elevations.
For slope, the first part (slope1) should be weighted with an importance of around 50-60%. For elevation, the second part (elevation2) should be weighted with about 65-75% importance.
In practice, the recommendation is to either just know the tendencies to make better guesses when a 2-plane surface putt appear on the course. It is also possible to instead simply do the average for the slope and do a 67% or 75% weighting (depending on what makes the easiest calculation) for elevation like the the following:
ElevationEstimate = elevation1*0.25 + elevation2*0.75.
ElevationEstimate = elevation1*0.33 + elevation2*0.67.
Currently there are no features in tGAT which allows for practise of 2-plane reads but it will appear in a future update.

2 thoughts on “2-plane green reading”